최근들어 취미로 여러 센서류를 사서 가지고 놀기위해 데이터 시트를 확인하다보니
항상 2의 보수(two's complement)라는 말에서 구글 검색창을 열었던 기억이 있어요.

2의 보수가 정확히 무엇일까?
2의 보수는 왜 2의 보수라고 하는가?
와 같은 궁금증들이 갑자기!! 생겼습니다. 한번 알아보죠.
Θ 보수란 무엇인가?
보수는 수학적으로 보충해주는 수라고 표현합니다.
즉, 3에 대한 15의 보수는 12, 10에 대한 13의 보수는 3이 됩니다.
Θ 컴퓨터에서는 보수를 왜 사용하는가?
결론부터 말하자면 컴퓨터가 0 과 1로 동작되기 때문에 2진수를 사용하죠. 그런데 2진수를 사용하면 음수(-)에 대한 처리가 불가능하여 보수를 사용하게 되었어요. 또한 보수를 사용하면 컴퓨터에서 뺏셈을 하기가 용이해요.
그래서 음수(-)에 대한 처리를 하기 위해서 최상위 비트(MSB)를 보통 부호 비트로 사용하기로 했었죠.
근데 단순이 최상위 비트(MSB)를부호 비트로 사용하면 산술연산시 문제가 발생했어요.
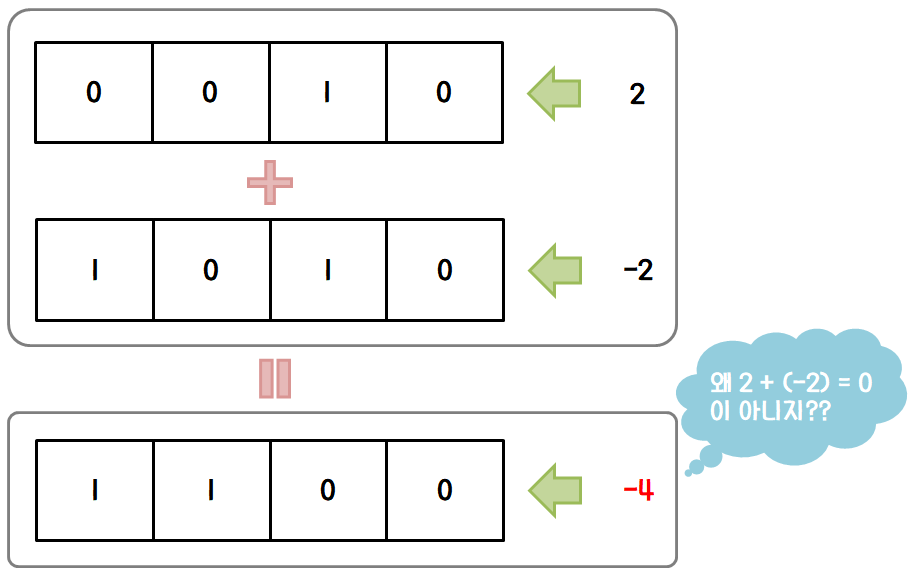
2와 -2를 더해보니 0이 아닌 -4가 나온 것이였죠.
=>0010(2) + 1010(-2) = 1100(-4)
그래서 보수의 개념이 사용되어지기 시작합니다.
Θ 1의 보수(one's complement)는 무엇이며 2의 보수(two's complement)는 무엇인가?
1의 보수(one's complement)는 원하는 비트에 not(~)을 한 것이예요.
0010(2) 의 1의 보수(one's complement)는 1101(-2) 와 같이 표현할 수 있죠.
1의 보수(one's complement)는 최상위 비트(MSB)를 부호 비트를 쓰는 방식보다 문제가 없었어요.
그런데 1의 보수(one's complement)를 사용하면 두수의 합이 0 일때 문제가 발생해요.
0010(2) + 1101(-2) = 1111(0?) 이 나와요.
맞아요. 1의 보수(one's complement)에서는 음의 0, 양의 0 이렇게 0이 두개로 나눠져서 문제가 발생했어요.

그러다보니 1의 보수(one's complement)의 문제를 해결하기 위해 2의 보수(two's complement)를 사용하게 됩니다.
2의 보수(two's complement)는 1의 보수(one's complement)에 +1을 한 값이예요.
0010(2) 의 2의 보수(two's complement)는 1110(-2) 가 되는 거죠.

이렇게 2의 보수(two's complement)를 하면 산술연산시 문제가 발생하지 않아 현재 잘 사용되고 있어요.
그 이외의 보수의 종류
* 숫자 N에 대한
* 숫자의 x진법
* 숫자의 y자리수
N의 x의 보수
=> x^y -N
N의 x-1의 보수
=> (x^y - 1) -N
ex) 10진수 120 의 10의 보수와 9의 부수는?
=> 10의 보수: 10^3 - 120 = 1000 - 120 = 880
=> 9의 보수: (10^3 -1) - 120 = 999 - 120 = 879
★핵심 내용★
즉, 컴퓨터 과학에서의
* 1의 보수는 ~x (0과 1을 반전)
* 2의 보수는 ~x + 1 (0과 1을 반전하고 +1)
이제부터라도 잊어버리지 말고 꼭 기억하자!!!
